A point on a curve where the slope = 0
A critical point is usually a local (or global) maxima or minima of a function. It is possible, though, such as in the case of x^3, that a critical point is neither a maxima or minima.
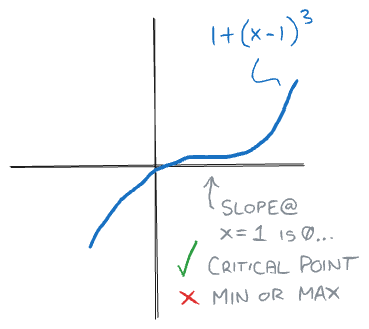
Can be found by taking the Derivative of the function, then finding where the result is equal to zero. 2x = 0 @ x=0… so x=0 is a Critical Point. In this case, it’s also a local and global minima.
Source
- School.