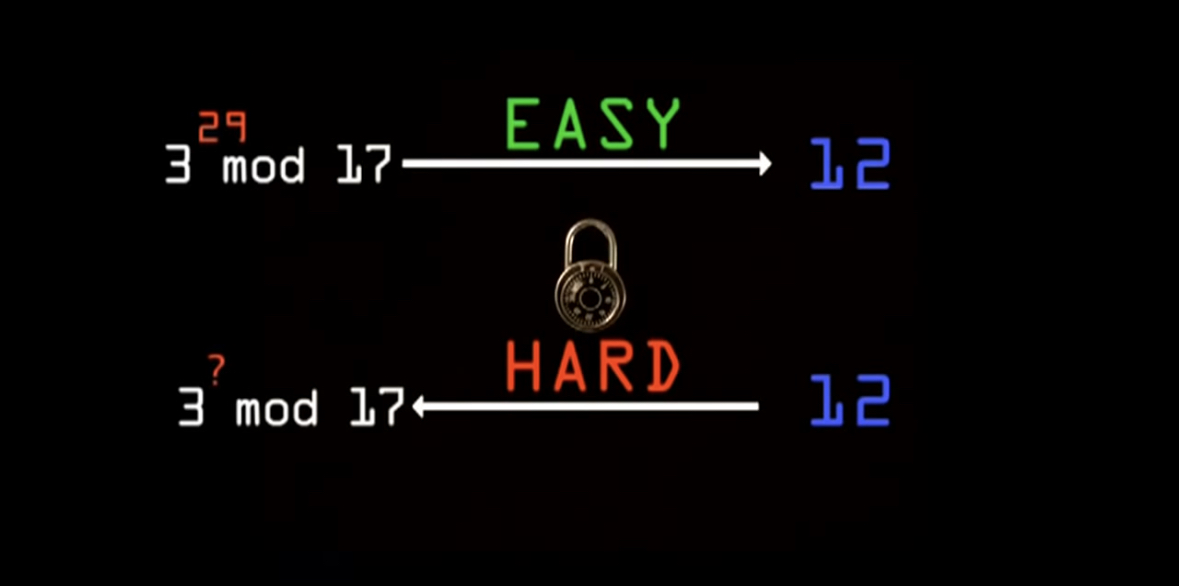
An import concept in Public Key Encryption
Primitive Root is a thing one number can be of another number. This deals with Prime Numbers and Modular Arithmetic. When used in the context of Public Key Encryption, the Primitive Root of the Modular operation is called the ’generator‘.
The definition of “primitive root” is a bit to opaque for me to glean without the examples below, but it’s:
A primitive root mod n is an integer g such that every integer Relatively Prime to n is congruent to a power of g mod n.
This makes a lot more sense in the examples below, from the source video:

2 is a primitive root of 5 because 2^1 mod 5 all the way through 2^(5-1) mod 5 give unique values.
Same can be said for 3 is a primitive root of 7:

And, to show that not all primes are primitive roots of each other - 2 is NOT a primitive root of 7:

So what
With a Primitive Root, you get a uniform distribution when raising the ”generator” to any integer power (X) modulus the prime number.
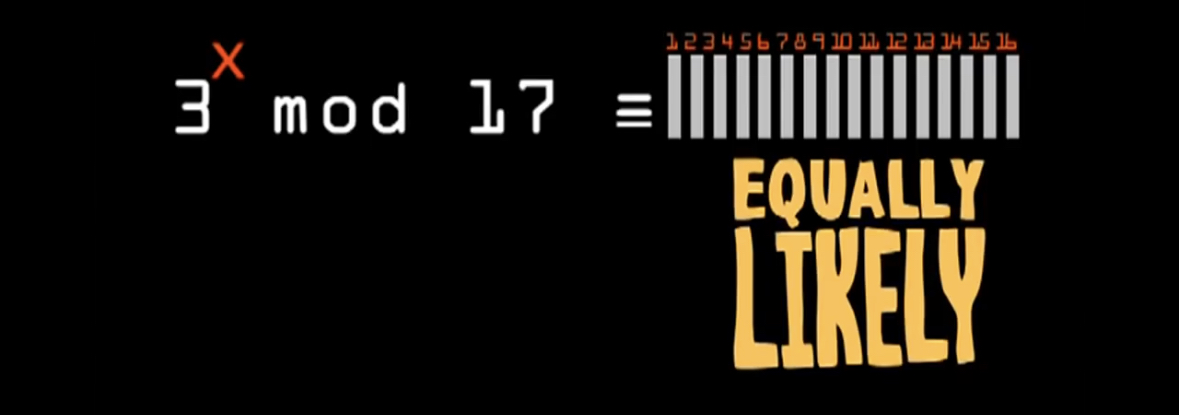
Given the congruent result, finding the exponent is computationally hard to do. It is a One-Way Function: